Recently, I was having a lovely Sunday breakfast with my even lovelier girlfriend Jessica and she was boiling some lovely eggs. She likes them a little bit more firm, so she boiled her for eight minutes. I had two runny eggs that have been boiled for six minutes. That’s sound like a pretty normal Sunday, right? That’s when our breakfast turned into a game show:
My girlfriend put, by accident, all three eggs in the same bowl with no way to distinguish between them. I, the game show host I am, had my girlfriend choose an egg and put it on her plate. Once she made her choice, I opened up one of the remaining eggs and of course, it was perfectly runny, just like the 6-minute egg I asked for. Then, I asked my girlfriend whether she wants to keep the egg she chose earlier or wants to switch to the egg that is still left. What should she do in order to get her hard-boiled egg?
That is a riddle that actually a lot of very smart people discussed about. This situation is very similar to the game show “Let’s make a deal” and the problem was first formulated by Steve Selvin. The procedure of the game show is somehow the following: A contestant is standing in front of three gates, one containing a prize and two containing a goat (or a Zonk in the German version, a red rat-like stuffed animal). Once the contestant chooses their gate, the host opens another gate containing a goat/Zonk and asks the contestant whether they want to switch their gate for the remaining gate. And the answer is (or at least should be) always yes.
The simplest explanation why one should always switch is, that when the contestant chooses their gate in the first round, they have a one in three (33%) chance of picking the prize. And that’s their chance of winning the game when they stick with it. However, when they are asked to switch gates, they only have two gates to choose from, so their chances of picking the right gate is 50%. So one should always switch when asked. Sounds counterintuitive? That’s because it is! And you’re not the only one to think so. World famous mathematician Paul Erdős didn’t believe it either until he saw numerical simulations.
But does our little Sunday-breakfast situation also follow the same logic? Let’s think about it.
At the start, my girlfriend chooses an egg. The chances that she picks her hardboiled egg is obviously 1/3. In that scenario, I have no other choice than to open one of my runny eggs. When I then ask her whether to change or not, she should obviously stay with her choice.
In the other scenario, the chances of her picking a runny egg is 2/3. After that I have a 50/50 chance of opening a hard boiled or runny egg. If I open her hard boiled egg, the game is over and she does not even get the chance to switch eggs. In the case I open one of my eggs, she ends up in a situation in which she should switch eggs. Both of these cases have a likelihood of 2/3 * 1/2 = 1/3.
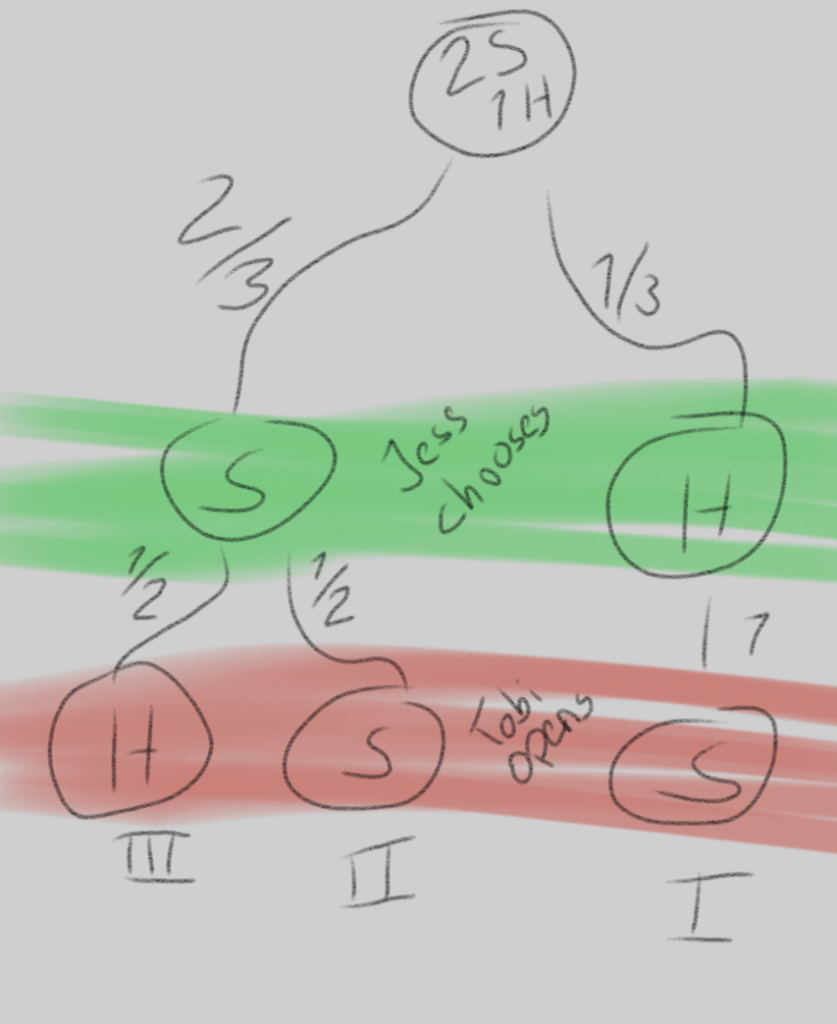
So in total there are three potential situations for Jessica:
I.) With a chance of one in three she makes the right choice initially. In this case she should stay with her choice.
II.) With a chance of one in three she makes the wrong choice initially and I then open a soft egg. In this case she should stay.
III.) With a chance of one in three she makes the wrong choice initially and I then open her hard egg. In this case she does not have a choice at all.
We see that out of the two scenarios in which she is offered the option to switch, one time she should take it and one time she should not. And both of these scenarios are equally likely. But didn’t we just say that the candidate in “Let’s make a deal” should always switch? What did we miss?
The difference is that Monty Hall, the host of the game show and the reason this whole thing is called the “Monty Hall Problem”, always knows in which gate there is a goat and he uses that knowledge to never open a gate with a goat in it.
Transferring that to our breakfast situation, I would need to know which one of the eggs is the hard one. That way, I could always open up a soft egg in the second stage, which would have Jessica end up in situation I with a chance of 1/3 and in situation II with a chance of 2/3, but never in situation III.
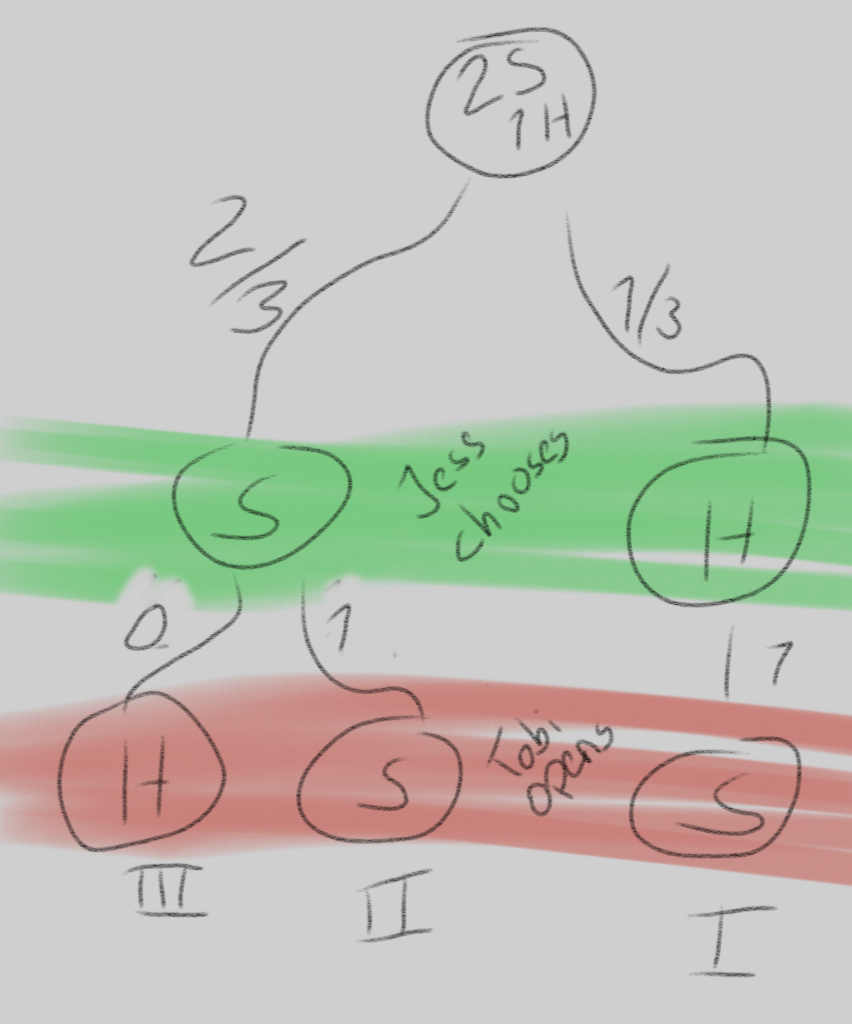
So, the initial question of whether or not Jessica should switch her egg is basically a question of whether I know which egg is the hard one. If so, she should better switch. If not, it does not matter.
But if any of us would know which egg is the hard boiled one, we would not have even ended up in this situation, right?